Journal of Biomechanical Engineering, 104, 6-11, (1982). Get pdf
Biomechanics II: Bone viscoelasticity, bone creep, bone relaxation
|
|
|
|

 The small dark circles in the human bone are cross sections of Haversian canals. The large circles are cross sections of osteons, which are large fibers about 200 microns across. Bovine plexiform has a laminated structure. Bone has a hierarchical structure in which each structural element itself contains structure.
The small dark circles in the human bone are cross sections of Haversian canals. The large circles are cross sections of osteons, which are large fibers about 200 microns across. Bovine plexiform has a laminated structure. Bone has a hierarchical structure in which each structural element itself contains structure.Summary on bone viscoelasticity
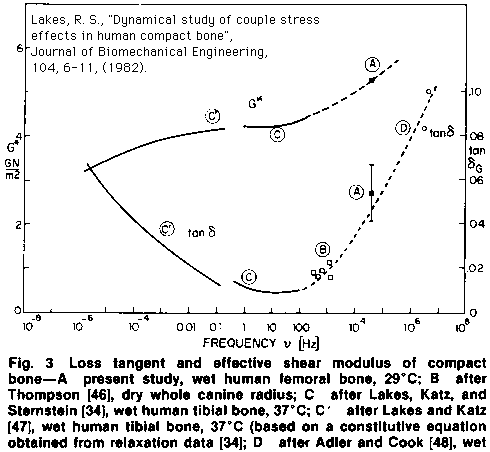
Bone exhibits viscoelastic behavior, i.e. the stress depends not only on the strain but also on the time history of the strain. Such behavior can manifest itself as creep, which is a gradual increase in strain under constant stress; stress relaxation, which is a gradual decrease in stress in a specimen held at constant strain; load-rate dependence of the stiffness; attenuation of sonic or ultrasonic waves; or energy dissipation in bone loaded dynamically. Experimental rheology modalities based on each of the above phenomena have been used in the study of bone. The results have been converted to a common representation via the interrelationships inherent in the linear theory of viscoelasticity, to permit a direct comparison of results. In the case of tension / compression, there is very significant disagreement among the published results. This disagreement may result from nonlinear viscoelastic behavior not accounted for in the transformation process, or from experimental artifacts. In the case of shear deformation, however, there is good agreement between results obtained in different kinds of experiments. The loss tangent, which is proportional to the ratio of energy dissipated to energy stored in a cycle of deformation, achieves a minimum value of about 0.01 at frequencies from 1 to 100 Hz. At lower and higher frequencies, the loss tangent, hence the magnitude of viscoelastic effects, is greater, e.g. 0.08 at 1 MHz and at one micro-Hz. To compare, the loss tangent of quartz may be less than one part per million, in metals, from one part in ten thousand to 0.01, in hard plastics from 0.01 to 0.1, and in soft polymers, it may attain values greater than 1. It is notable that the minimum energy dissipation in bone occurs in a frequency range characteristic of load histories during normal activities.
Lakes, R. S. and Katz, J. L., "Interrelationships among the viscoelastic functions for anisotropic solids: application to calcified tissues and related systems." Journal of Biomechanics, 7, 259-270, (1974).
Lakes, R. S. and Katz, J. L., "Transformation of the viscoelastic functions of calcified tissues and interfacial biomaterials in a common representation," Journal of Biological Physics, 2, (4) 193-204, (1974).
Lakes, R. S. and Katz, J. L., "Dielectric relaxation in cortical bone," Journal of Applied Physics, 48, 808-811, (1977).
Saha, S. and Lakes, R. S., "A non-invasive technique for detecting stress waves in bone using the piezoelectric effect," IEEE Transactions on Biomedical Engineering, BME-24, 508-512, (1977).
Saha, S. and Lakes, R. S., "The effect of soft tissue on wave propagation and vibration tests for determining the in vivo properties of bone," Journal of Biomechanics, 10, 398-401, (1977).
Lakes, R. S. and Katz, J. L., "Viscoelastic and dielectric properties of bone," Bulletin of the Hospital for Joint Diseases, New York, 38 (1), 23-24, (1977).
Lakes, R. S. and Saha, S., "A non-contacting electromagnetic device for the determination of in vivo properties of bone." Medical Instrumentation, 12 (2), 106-109, (1978). abstract
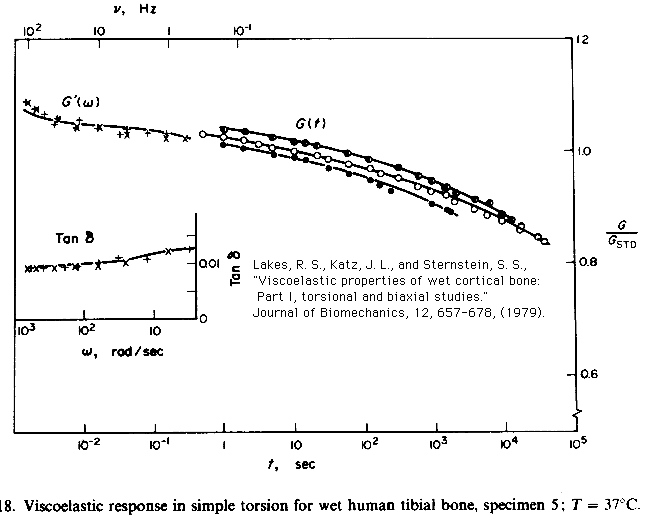
Lakes, R. S., Katz, J. L., and Sternstein, S. S., "Viscoelastic properties of wet cortical bone: Part I, torsional and biaxial studies." Journal of Biomechanics, 12, 657-678, (1979). get pdf
Lakes, R. S., Katz, J. L., "Viscoelastic properties of wet cortical bone:
Part II, relaxation mechanisms," Journal of Biomechanics, 12, 679-687, (1979). get pdf
Lakes, R. S. and Katz, J. L., "Viscoelastic properties of wet cortical bone:
Part III, A non-linear constitutive equation," Journal of Biomechanics, 12, 689-698, (1979). get pdf
Lakes, R. S. and Saha, S., "Cement line motion in bone," Science, 204, (1979), 501-503. Get article get pdf
Compact bovine bone subjected to constant torsional load for long periods of time exhibits large anelastic effects. Displacements occur at the cement lines and are responsible for part or all of the long term deformation. The absence of an asymptotic creep strain is consistent with an interpretation of the cement line as a viscous interface.
Lakes, R. S., "The role of gradient effects in the piezoelectricity of bone",
IEEE Trans. Biomed. Eng., BME-27 (5), 282-283, (1980).
Lakes, R. S., and Saha, S. "Long-term torsional creep in compact bone,"
Journal of Biomechanical Engineering, 102, 178-180, (1980). abstract
Yang, J. F. C., and Lakes, R. S., "Transient study of couple stress in compact bone: torsion", Journal of Biomechanical Engineering, 103, 275-279, (1981). Get pdf. abstract
Lakes, R. S., "Dynamical study of couple stress effects in human compact bone",
Journal of Biomechanical Engineering, 104, 6-11, (1982). Get pdf

Yang, J. F. C., and Lakes, R. S., "Experimental study of micropolar and couple stress
elasticity in bone in bending", Journal of Biomechanics, 15, 91-98, (1982). Get pdf
Summary: bone as a composite material
Early composite models for bone were two-phase models involving the mineral and protein phases only. At the ultrastructural level one may imagine the mineral crystals as a particulate reinforcing phase and the surrounding collagen as a matrix phase. Strong arguments were presented that bone cannot be described simply as a compound bar or as a material similar to prestressed concrete. Based on measured Young's moduli of 114 GPa for hydroxyapatite and 1.2 GPa for collagen derived from tendon , rigorous upper and lower bounds on the elastic modulus of compact bone were calculated by Katz. Young's modulus of bone lay between these bounds and was less than the value obtained by a simple rule of mixtures approach. Similar comparisons were made for other natural collagen-apatite composites such as dentin and enamel from human teeth. More recently, composite models have been developed which incorporate the structure of Haversian bone, with the osteons viewed as hollow fibers embedded in a matrix. The matrix is the ground substance which comprises the cement lines between osteons and is thought to be principally composed of mucopolysaccharides. The stiffness of the ground substance have not been determined experimentally but it has been inferred from a composite model in conjunction with experimental data from ultrasound studies by Katz on whole bone. The ground substance was computed to be about one quarter as stiff as the osteon itself. The view of the ground substance as a compliant interface is also supported by the results of several experimental studies. Localized slippage occurs at the cement lines in specimens of bovine plexiform bone of human Haversian bone subjected to prolonged stress. Under such conditions, the ground substance at the cement lines appears to behave in a viscous manner. Considering the full range of load rates and frequencies, one may view the ground substance as a compliant and highly viscoelastic material. Such a conclusion is perhaps surprising in view of the fact that the ground substance is highly mineralized. Nevertheless a view of the ground substance as a compliant interface is supported by further experiments. For example, studies of single osteons and osteon groups in torsion have revealed size effects to occur and the osteon to have a higher effective shear modulus than whole bone. Similar size effects were observed in torsional and bending experiments upon larger microsamples. These latter results have been interpreted in light of a generalized form of elasticity theory, known as Cosserat elasticity, which admits both strain of the material and local rotations of microscopic constituents, e.g. the osteons. A twist per unit area or couple stress can occur in addition to a force per unit area or couple stress.By contrast, classical elasticity, which describes most ordinary materials, involves only strains and stresses. Cosserat elasticity is likely to differ significantly from classical elasticity in its predictions of stress and strain around holes, cracks, and interfaces. For large, whole bones, conventional anisotropic elasticity has been shown to be entirely adequate.
Lakes, R. S., Yoon, H. S. and Katz, J. L., "Slow compressional wave propagation
in wet human and bovine cortical bone", Science, 220 513-515, (1983). Get article pdf
Park, H. C. and Lakes, R. S., "Cosserat micromechanics of human bone: strain redistribution by a hydration-sensitive constituent", J. Biomechanics, 19 385-397 (1986).
Experimental determination of the strain distribution in prismatic, square cross section bars of human compact bone in torsion disclosed nonclassical effects associated with the microstructure. Specifically, in wet bone at small strain, significant deviations from the classically predicted strain distribution were observed. The measured strain distribution in wet bone followed predictions based on Cosserat (micropolar) elasticity. In dry bone, the strain distribution was very close to the prediction of classical elasticity. The interaction between Haversian osteons and the cement substance between them was hypothesized to be the principal mechanism for the phenomena. To evaluate this hypothesis, additional specimens were subjected to prolonged torsional load and the cement lines were observed by reflected light microscopy. Localized deformation at the cement lines was observed, but it was less than values reported earlier for bovine plexiform bone. Get pdf.
Lakes, R. S., Yoon, H. S. and Katz, J. L., "Ultrasonic wave propagation and attenuation in wet bone," J. Biomed. Engng., 8 143-148 (1986).
Lakes, R. S. "Properties of bone and teeth," in Encyclopedia of Medical Devices and Instrumentation, ed. J.G. Webster, J. Wiley, NY, 501-512 (1988).
Bone has a variety of functions in the body of which some of the most important are structural in nature: protection of vulnerable body parts, support of the body, and to provide muscle attachments. A knowledge of the mechanical and adaptive properties of bone is useful in the design and use of prostheses which replace a bone or a portion of a bone. Mechanical properties of bone are also of interest in trauma biomechanics and in efforts to prevent injury to the body. As for teeth, they also are replaced by artificial materials which are called upon to perform the mechanical functions of the original tooth. This article contains a survey of known properties of bone and teeth, with an emphasis on bone and its mechanical properties.
Lakes, R. S., Nakamura, S., Behiri, J. C. and Bonfield, W., "Fracture mechanics of bone with short cracks", Journal of Biomechanics, 23, 967-975 (1990).
Tensile fracture experiments were performed upon specimens of wet mature bovine Haversian bone, with short, controlled notches. Stress concentration factors were found to be significantly less than values predicted using a maximum stress criterion in the theory of elasticity. Results were also modeled with the aid of linear elastic fracture mechanics. Agreement of experiment with theory was better in this case, however deviations were seen for short notches. Two mechanisms were evaluated for the behavior: plasticity near the crack tip, and effects of the Haversian microstructure, modelled by Cosserat elasticity, a generalized continuum theory. Plastic zone effects were found to be insignificant. Cosserat elasticity, by contrast, predicted stress concentration factors which better approximated observed values. To explore strain redistribution processes, further experiments were conducted upon notched specimens in torsion at small strain. They disclosed a strain redistribution effect consistent with Cosserat elasticity. These microelastic effects are attributed to the Haversian architecture of bone.
Magnusson M., Aleksiev A., Spratt K., Lakes R. S., Pope M. H., "Hyperextension and spine height changes", Spine, 21(22), 2670-2675, (1996). abstract
Lakes, R. S., "On the torsional properties of single
osteons", J. Biomechanics, 28, 1409-1410, (1995).
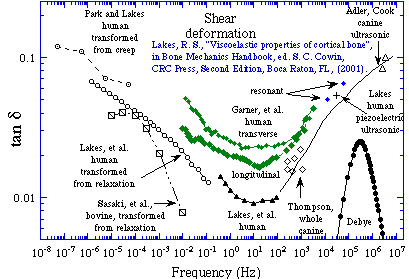 Axial damping summary graph, Shear damping summary graph.
Axial damping summary graph, Shear damping summary graph.|
|
| |