Meaning of Poisson's ratio

Rod Lakes
Search tool

Definition of Poisson's ratio
Poisson's ratio is the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force. Tensile deformation is considered positive and compressive deformation is considered negative. The definition of Poisson's ratio contains a minus sign so that normal materials have a positive ratio. Poisson's ratio, also called Poisson ratio or the Poisson coefficient, or coefficient de Poisson, is usually represented as a lower case Greek nu, n.
If your browser does not interpret Symbol font properly, Greek nu, n may instead look like a bold face Latin n. For an alternative page go here.

animation of stretching Poisson's ratio
n = - etrans / elongitudinal

Strain e is defined in elementary form as the change in length divided by the original length.
e = DL/L.

Poisson's ratio: why usually positive
Virtually all common materials, such as the blue rubber band on the right, become narrower in cross section when they are stretched. The reason why, in the continuum view, is that most materials resist a change in volume as determined by the bulk modulus K (also called B) more than they resist a change in shape, as determined by the shear modulus G.
stretch honeycomb effect of Poisson's ratioIn the structural view, the reason for the usual positive Poisson's ratio is that inter-atomic bonds realign with deformation. Stretching of yellow honeycomb by vertical forces, shown on the right, illustrates the concept. Negative Poisson's ratio in designed materials and in some anisotropic materials is by now well known.

Poisson's ratio: relation to elastic moduli in isotropic solids
Poisson's ratio is related to elastic moduli K (also called B), the bulk modulus; G as the shear modulus; and E, Young's modulus, by the following (for isotropic solids, those for which properties are independent of direction). The elastic moduli are measures of stiffness. They are ratios of stress to strain. Stress is force per unit area, with the direction of both the force and the area specified. See Sokolnikoff Ref. [1]; also further details.
n = (3K - 2G)/(6K + 2G)
E = 2G( 1 + n)
E = 3K(1 - 2 n)
Further interrelations among elastic constants for isotropic solids are as follows. B is the bulk modulus.
elasticity interrelations with Poisson's ratio 1 elasticity interrelations with Poisson's ratio 2 elasticity interrelations with Poisson's ratio 3
The theory of isotropic linear elasticity allows Poisson's ratios in the range from -1 to 1/2 for an object with free surfaces with no constraint. Physically the reason is that for the material to be stable, the stiffnesses must be positive; the bulk and shear stiffnesses are interrelated by formulae which incorporate Poisson's ratio. Objects constrained at the surface can have a Poisson's ratio outside the above range and be stable.

Poisson's ratio in various materials: table of Poisson's ratio
Poisson's ratio of the elements are, unless otherwise cited, via Web Elements, which adduce references [2-4]. In a large compilation of properties of polycrystalline materials [5], most have Poisson's ratio in the vicinity of 1/3. Some experiments, e. g. the resonant ultrasound studies in [9], provide cross-checking; comparison of multiple vibration mode frequencies confirms the modulus and Poisson's ratio follow linear isotropic elasticity.
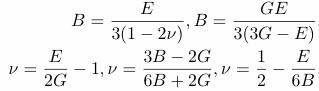
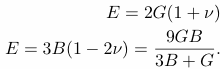
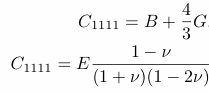
Material
Isotropic upper limit [1]
Rubber [6]
Indium [11]
Gold [4]
Lead [4]
Copper [7]
Aluminum [4]
Copper [4]
Polystyrene [6]
Brass [1]
Ice [8]
Polystyrene foam [6]
Stainless Steel [7]
Steel [1]
Tungsten [4]
Tungsten
Zinc [5]
Fused quartz [9]
Boron [12]
Beryllium [4]
Re-entrant foam [10]
Isotropic lower limit [1] 		Poisson's ratio
0.5
0.48- ~0.5
0.45
0.42
0.44
0.37
0.34
0.35
0.34
0.33
0.33
0.3
0.30
0.29
0.30
0.28
0.25
0.17
0.08
0.03
-0.7
-1 		References
[1] I. S. Sokolnikoff, Mathematical theory of elasticity. Krieger, Malabar FL, second edition, 1983.
[2] A. M. James and M. P. Lord in Macmillan's Chemical and Physical Data, Macmillan, London, UK, 1992.
[3] G.W.C. Kaye and T.H. Laby in Tables of physical and chemical constants, Longman, London, UK, 15th edition, 1993.
[4] G.V. Samsonov (Ed.) in Handbook of the physicochemical properties of the elements, IFI-Plenum, New York, USA, 1968.
[5] G. Simmons, and H. Wang, Single crystal elastic constants and calculated aggregate properties: a handbook, MIT Press, Cambridge, 2nd ed, 1971.
[6] J. A. Rinde, Poisson's ratio for rigid plastic foams, J. Applied Polymer Science, 14, 1913-1926, 1970.
[7] D. E. Gray, American Institute of Physics Handbook, 3rd ed., chapter 3, McGraw hill, New York, 1973.
[8] E. M. Schulson, The mtructure and mechanical behavior of ice, JOM, 51 (2) pp. 21-27, 1999. article link
[9] H. H. Demarest, Jr., Cube resonance method to determine the elastic constants of solids, J. Acoust. Soc. Am. 49, 768-775 (1971).
[10] R. S. Lakes,   Foam structures with a Negative Poisson's ratio, Science, 235 1038-1040, 1987.
[11] D. Li, T. M. Jaglinski, D. S. Stone, and R. S. Lakes, Temperature insensitive negative Poisson's ratios in isotropic alloys near a morphotropic phase boundary, Appl. Phys. Lett, 101, 251903, Dec. (2012).
[12] K. A. Gschneidner, Jr., Physical Properties and Interrelationships of Metallic and Semimetallic Elements, Solid State Physics, 16, 275-426, 1964
Further confirmation of consistency of the low Poisson's ratio (as 0.05) of beryllium was provided in A. Migliori, H. Ledbetter, D. J. Thoma, and T. W. Darling, "Beryllium's monocrystal and polycrystal elastic constants", J. Applied Physics 95, 2436- 2440 (2004). Beryllium has the lowest Poisson's ratio for any polycrystalline metal. Elastic constants were measured for both single crystals and polycrystalline samples. Beryllium does not obey the Cauchy relations, so non-central forces between atoms were inferred.

Poisson's ratio in bending.
Bend a bar or plate. Poisson's ratio governs the curvature in a direction perpendicular to the direction of bending. This "anticlastic curvature" is easily seen in the bending of a rubber eraser. Shown here is bending, by a moment applied to opposite edges, of a honeycomb with hexagonal cells. If the honeycomb cells are regular hexagons, the Poisson's ratio can approach +1. Since the honeycomb is anisotropic, the Poisson's ratio need not lie within the above range. bend honeycomb effect of Poisson's ratio

Poisson's ratio and anisotropy.
In anisotropic solids including single crystals, honeycombs, and fibrous composites, physical properties, including Poisson's ratio and elastic moduli, depend on direction. Poisson's ratio can have positive or negative values of arbitrarily large magnitude in anisotropic materials.
For orthotropic materials, Poisson's ratio is bounded by the ratio of Young's moduli E as follows.
|n 12| < (E1 /E2 )1/2
B. M. Lempriere "Poisson's ratio in orthotropic materials" AIAA Journal, 6, No. 11, 2226-2227 (1968)
Maximum and minimum Poisson's ratio values are derived in terms of the elastic compliances of materials with cubic symmetry.
Hayes, M., and Shuvalov, A., "On the Extreme Values of Young's Modulus, the Shear Modulus, and Poisson's Ratio for Cubic Materials", ASME J. Appl. Mech., 65, 786-787, (1998).

Poisson's ratio in viscoelastic materials
The Poisson's ratio in a viscoelastic material is time dependent in the context of transient tests such as creep and stress relaxation. If the deformation is sinusoidal in time, Poisson's ratio may depend on frequency, and may have an associated phase angle. Specifically, the transverse strain may be out of phase with the longitudinal strain in a viscoelastic solid. Get pdf of a research article on this. For polymers in the glassy regime, Poisson's ratio is on the order 1/3. At higher temperature (or at longer times or lower frequency) sufficient for rubbery behavior, the stiffness decreases greatly and Poisson's ratio approaches 1/2.

Poisson's ratio and phase transformations
Poisson's ratio can vary substantially in the vicinity of a phase transformation. Typically the bulk modulus softens near a phase transformation but the shear modulus does not change much. The Poisson's ratio then decreases in the vicinity of a phase transformation and can attain negative values. Phase transformations are discussed further on the linked page.

Poisson's ratio, waves and deformation
The Poisson's ratio of a material influences the speed of propagation and reflection of stress waves. In geological applications, the ratio of compressional to shear wave speed is important in inferring the nature of the rock deep in the Earth. This wave speed ratio depends on Poisson's ratio. Poisson's ratio also affects the decay of stress with distance according to Saint Venant's principle, and the distribution of stress around holes and cracks.

An example. Analysis of effect of Poisson's ratio on compression of a layer.
What about the effect of Poisson's ratio on constrained compression in the 1 (or x) direction? Constrained compression means that the Poisson effect is restrained from occurring. This could be done by side walls in an experiment. Also, compression of a thin layer by stiff surfaces is effectively constrained. Moreover, in ultrasonic testing, the wavelength of the ultrasound is usually much less than the specimen dimensions. The Poisson effect is restrained from occurring in this case as well.
In Hooke's law (with the elastic modulus tensor as Cijkl we sum over k and l, but, due to the constraint, the only strain component which is non-zero is e11.
sij= Cijklekl= C1111e11+ C1122e22+ C1133e33= C1111e11,

so the effective stiffness for constrained compression is C1111.

Let us find the physical significance of that tensor element in terms of engineering constants.

One may also work with the elementary isotropic form for Hooke's law.
exx= (1/E) {sxx- nsyy-nszz}
eyy =(1/E) {syy- nsxx-nszz}
ezz= (1/E) {szz- nsxx-nsyy}

For simple tension or compression in the x direction, the Poisson effect is free to occur. There is stress in only one direction but there can be strain in three directions. sxx≠ 0, that is not equal to zero, syy = 0, szz= 0. Then
(sxx/ exx)= E.
So Young's modulus E is the stiffness for simple tension, with the Poisson effect free to occur.

Consider constrained compression, with eyy= 0, ezz= 0. Then
syy= nsxx+nszz.
szz = nsxx+nsyy.
Substituting,
syy= szz= sxx(n(1+ n)/(1- n2)).
So,substituting into Hooke's law, the stress-strain ratio for constrained compression, which by definition is the constrained modulus C1111,is
(sxx/exx)= C1111= E ((1 - n) / (1 + n)(1 - 2n)).

The physical meaning of C1111is the stiffness for tension or compression in the x (or 1) direction, when strain in the y and z directions is constrained to be zero. The reason is that for such a constraint the sum in the tensorial equation for Hooke's law collapses into a single term containing only C1111. The constraint could be applied by a rigid mold, or if the material is compressed in a thin layer between rigid platens. C1111also governs the propagation of longitudinal waves in an extended medium, since the waves undergo a similar constraint on transverse displacement.

Rubbery materials have Poisson's ratios very close to 1/2, shear moduli on the order of a MPa, and bulk moduli on the order of a GPa. Therefore the constrained modulus C1111is comparable to the bulk modulus and is much larger than the shear or Young's modulus of rubber.

Practical example - cork in a bottle.
An example of the practical application of a particular value of Poisson's ratio is the cork of a wine bottle. The cork must be easily inserted and removed, yet it also must withstand the pressure from within the bottle. Rubber, with a Poisson's ratio of 0.5, could not be used for this purpose because it would expand when compressed into the neck of the bottle and would jam. Cork, by contrast, with a Poisson's ratio of nearly zero, is ideal in this application.

Practical example - design of rubber buffers.
How does three-dimensional deformation influence the use of viscoelastic rubber in such applications as shoe insoles to reduce impact force in running, or wrestling mats to reduce impact force in falls?
Solution
Refer to the above analysis, in which deformation under transverse constraint is analyzed. Rubbery materials are much stiffer when compressed in a thin layer geometry than they are in shear or in simple tension; they are too stiff to perform the function of reducing impact. Compliant layers can be formed by corrugating the rubber to provide room for lateral expansion or by using an elastomeric foam, which typically has a Poisson's ratio near 0.3, in contrast to rubber for which Poisson's ratio can exceed 0.49. Corrugated rubber is used in shoe (sneaker) insoles and in vibration isolators for machinery. Foam is used in shoes and in wrestling mats.

squeeze block Poisson's ratio effectPractical example - aircraft sandwich panels.
The honeycomb shown above is used in composite sandwich panels for aircraft. The honeycomb is a core between face-sheets of graphite-epoxy composite. Such panels are usually flat. If curved panels are desired, the honeycomb cell shape must be changed from the usual regular hexagon shape, otherwise the cells will be crushed during bending. Several alternative cell shapes are known, including those which result in a negative Poisson's ratio.

Practical example - Interpreting compression tests on blocks of flexible material.
The material is constrained at contact surfaces by the compression device, so the Poisson effect cannot freely occur. Bulge occurs in the middle as shown in the image on the right. The experiment does not provide Young's modulus E. The definition of Young's modulus E entails freedom from transverse constraint but the block is short enough that constraint by the contact surfaces is pertinent. Determination of the elastic modulus E involves use of correction formulae that depend on Poisson's ratio.

A review article with materials science emphasis:
Greaves, G. N., Greer, A. L., Lakes, R. S., and Rouxel, T., "Poisson's Ratio and Modern Materials", Nature Materials, 10, 823-837 Nov. (2011). In comparing a material's resistance to distort under mechanical load rather than alter in volume, Poisson's ratio offers the fundamental metric by which to compare the performance of any material when strained elastically. The numerical limits are set by 1/2 and -1, between which all stable isotropic materials are found. With new experiments, computational methods and routes to materials synthesis, we assess what Poisson's ratio means in the contemporary understanding of the mechanical characteristics of modern materials. Central to these recent advances, we emphasize the significance of relationships outside the elastic limit between Poisson's ratio and densification, connectivity, ductility and the toughness of solids; and their association with the dynamic properties of the liquids from which they were condensed and into which they melt. get pdf.

Lakes, R. S., "Negative-Poisson's-Ratio Materials: Auxetic Solids", Annual Review of Materials Research, 47: 63-81 July (2017).
Poisson's ratio had long been considered to be an intrinsic material property, confined within a narrow domain and governed solely by the geometry of interatomic bonds. Materials with designed heterogeneity allow control over the Poisson's ratio. Poisson's ratios of any value within the thermodynamically admissible domain may be attained, including negative Poisson's ratio (called auxetic). In this article, we discuss the role of Poisson's ratio in elasticity, two-dimensional and three dimensional materials, phase transformations, underlying causes in the microstructure and other negative physical properties.
journal link. journal reprint link

Google iconGoogle bookmark
Rod Lakes home return

Negative Poisson's ratio       Phase transformations

Negative stiffness inclusions
Top