Chiral metamaterials

Summary
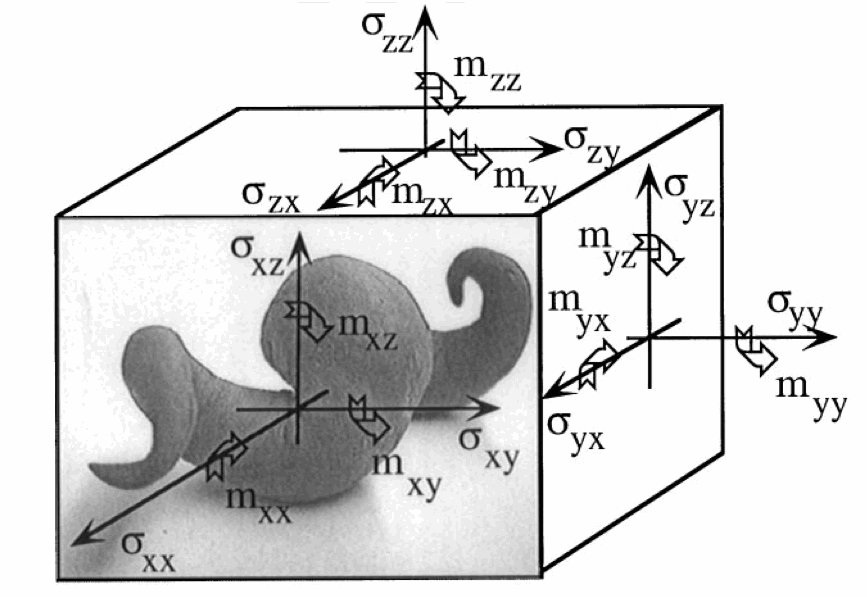
A solid which is isotropic with respect to coordinate rotations but not with respect to inversions is called noncentrosymmetric, acentric, hemitropic, or chiral. Chirality (hemitropy) has no effect upon the classical elastic modulus tensor. In Cosserat elasticity, chirality has an effect. Asymmetric stress is allowed in Cosserat solids.
A chiral or hemitropic micropolar cylindrical rod is predicted to undergo torsional deformation when subjected to tensile load, so a chiral material will twist when stretched. It will also twist when compressed. Classical elasticity cannot account for such phenomena. These concepts lay the groundwork for chiral metamaterials or chiral architectured materials or chiral architected materials; we did not use such terminology. Such materials can be made by 3D printing or by other methods. Indeed the first known materials observed to exhibit chiral elastic effects were natural.
The theoretical groundwork for chiral elastic materials was developed here.
R. S. Lakes and R. Benedict, Noncentrosymmetry in Micropolar Elasticity, International Journal of Engineering Science, 20 (10), 1161-1167, (1982).
Download a pdf of this article.
Experimental stretch twist coupling of bone specimens was presented in
R. S. Lakes, Is bone elastically noncentrosymmetric?, Proc. 34th ACEMB. Houston (1981).
Get pdf.
This is likely the first observation of elastic chirality in a material.
Lakes, R. S., "Elastic and viscoelastic behaviour of chiral materials", Int. J. of Mechanical Sciences, 43, 1579-1589, June (2001).
Chiral materials are not invariant to inversions: there is a distinction between right and left handed material. Material properties such as piezoelectricity and pyroelectricity, represented by tensors of odd rank, can only occur in chiral materials. Chiral effects in elasticity cannot be expressed within classical elasticity since the modulus tensor, which is fourth rank, is unchanged under an inversion. We consider effects of chirality in elastic materials described by a generalized continuum representation, specifically Cosserat elasticity. Analysis of several configurations discloses a chiral material to generate reaction moments when compressed as a slab. A chiral plate bent to hyperbolic shape is predicted to exhibit size effects from the Cosserat characteristic length, and a shear force from the chirality. This analysis can be used for the interpretation of experiments on compliant chiral materials, in particular the evaluation of the elastic constants. Viscoelastic chiral solids are examined in the context of the correspondence principle. Chiral solids exhibit stretch twist coupling.
Download pdf here.
Ha, C. S., Plesha, M. E., Lakes, R. S., "Chiral three dimensional lattices with tunable Poisson's ratio, Smart Materials and Structures, 25, 054005 (6pp) (2016).
Chiral three dimensional cubic lattices are developed with rigid cubical nodules and analyzed via finite element analysis. The lattices exhibit geometry dependent Poisson's ratio that can be tuned to negative values. Poisson's ratio tends to zero as the cubes become further apart. The lattices exhibit stretch twist coupling. Such coupling cannot occur in a classical elastic continuum but it can occur in a chiral Cosserat solid.
journal link.
preprint pdf
 Ha, C. S., Plesha, M. E., Lakes, R. S., Chiral three-dimensional isotropic lattices with negative Poisson's ratio, Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055
Ha, C. S., Plesha, M. E., Lakes, R. S., Chiral three-dimensional isotropic lattices with negative Poisson's ratio, Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055
Chiral three-dimensional isotropic cubic lattices with rigid cubical nodules and multiple deformable ribs are developed and analyzed via finite element analysis. The lattices exhibit geometry dependent Poisson's ratio that can be tuned to negative values. Poisson's ratio decreases from positive to negative values as the number of cells increases. Isotropy is obtained by adjustment of aspect ratio. The lattices exhibit significant size effects. Such a phenomenon cannot occur in a classical elastic continuum but it can occur in a Cosserat solid. The material exhibits squeeze-twist coupling and stretch-twist coupling.
This is the first three-dimensional metamaterial that is chiral; we did not call it by such a name. It also may be called a truss metamaterial.
journal link. Figure on cover link
preprint pdf
Buchanan, K., Lakes, R.. S., Vanderby, R., "Chiral behavior in rat tail tendon fascicles", Journal of Biomechanics, 64, 206-211 7 Nov. (2017).
Journal link
Single fascicle nonlinear stretch-twist coupling is observed. Such stretch-twist coupling and size dependence cannot be understood via classical elasticity but is predicted by Cosserat (micropolar) elasticity. Tendon fascicles are chiral based on observed axial load-induced twist. A helical fascicle structure is implied and is supported by microscopic observation.
get preprint pdf
D. Reasa and R. S. Lakes, "Cosserat effects in achiral and chiral cubic lattices", Journal of Applied Mechanics (JAM), 86, 111009-1, 6 pages Nov. (2019).
Cubic 3D lattices were designed, made by 3D printing, and studied experimentally. One lattice was simple cubic with ribs of diameter 1/5 the cell size. The second lattice was chiral, with spiral ribs. The chiral lattice, but not the achiral lattice, exhibited squeeze-twist coupling with size effects. Squeeze-twist coupling cannot occur in a classically elastic solid but is anticipated by theory in a Cosserat solid. Both lattices exhibited size effects in bending and torsion. These also may be called truss metamaterials.
https://doi.org/10.1115/1.4044047 https://doi.org/10.1115/1.4044047
J. Li, C. S. Ha, R. S. Lakes, "Observation of squeeze twist coupling in a chiral three-dimensional isotropic lattice", Physica Status Solidi B : Basic Solid State Physics. 257, (10), 1900140, October (2020).
journal link
A chiral 3D lattice was designed, made by 3D printing, and studied experimentally. The lattice exhibited squeeze-twist coupling and a Poisson's ratio near zero. Squeeze-twist coupling does not occur in classical elasticity which makes no provision for chirality. By contrast, chiral effects are allowed in Cosserat elasticity. An experimental squeeze-twist coupling strain ratio on the order of unity and a Poisson's ratio near zero are in reasonable agreement with prior finite element analysis of a lattice with similar structure, for which negative Poisson's ratio is anticipated for a sufficient number of cells.
D. R. Reasa and R. S. Lakes, Nonclassical Chiral Elasticity of the Gyroid Lattice, Phys. Rev. Lett. 125, 205502, 13 November (2020).
The gyroid lattice is a metamaterial which allows chirality that is tunable by geometry. Gyroid lattices were made in chiral and non-chiral form by 3D printing. The chiral lattices exhibited nonclassical elastic effects including coupling between compressive stress and torsional deformation. Gyroid lattices can approach upper bounds on elastic modulus. Effective modulus is increased by distributed moments but is, for gyroid cylinders of sufficiently small radius, softened by a surface layer of incomplete cells. Such size dependence is similar to that in foams is but unlike most lattices.
journal link
preprint pdf
R. S. Lakes, B. Huey, and K. Goyal,"Extended Poisson's ratio range in chiral isotropic elastic materials", Physica Status Solidi B 259, (12), 2200336 (2022).
https://doi.org/10.1002/pssb.202200336
Poisson's ratio in chiral Cosserat elastic solids is considered. Chirality allows the Poisson's ratio to exceed classical bounds, even if the material is directionally isotropic and all elastic moduli are within thermodynamic limits based on strain energy density. Poisson's ratio in chiral rods depends on the chiral elastic constants as well as on the shear and bulk moduli, assumed positive. Poisson's ratio can be greater than 0.5 or smaller than -1 for slender chiral specimens.
preprint pdf doi link
T. DeValk, J. Hestetune, R. S. Lakes,"Nonclassical thermal twist of the chiral gyroid lattice", Physica Status Solidi B 259, (12), 2200338 (2022).
The gyroid lattice was prepared in chiral and non-chiral forms. The chiral gyroid lattice was observed to exhibit temperature induced twist with direction of twist corresponding to the sense of chirality. This effect is a nonclassical effect that cannot occur in classical elasticity or classical thermo-elasticity but is allowable in Cosserat solids. Poisson's ratio of the gyroid is known to be about 0.3 with minimal dependence on size. In contrast to squeeze-twist coupling in which substantial size effects occur with slender specimens twisting much more than thicker ones, thermal-twist coupling exhibits opposite and less consistent size effects of much smaller magnitude.
https://doi.org/10.1002/pssb.202200338
W. Zhang, R. Neville, D. Zhang, J. Yuan, F. Scarpa, R. Lakes, "Bending of kerf chiral fractal lattice metamaterials", Composite Structures, 117068 , online 30 April (2023).
doi link https://doi.org/10.1016/j.compstruct.2023.117068
R. S. Lakes, "Poisson's ratio beyond the classically allowable range in chiral isotropic elastic materials: effect of kappa and experiment", Physica Status Solidi B
Poisson's ratio in chiral isotropic elastic solids can be larger or smaller than the classical thermodynamic bounds. The effect of Cosserat coupling constant k is studied. Analysis shows that solids with weak coupling exhibit Poisson's ratio anomalies for larger specimen sizes than corresponding solids with strong coupling. Experiments on a quasi-isotropic composite with chiral inclusions show Poisson's ratio greater than 0.5.
First published: 14 November (2023). pdf available via agreement between publisher and the university.
doi link
Chiral structures have been observed in trees by Professor Cherkaev of the Mathematics Department at the University of Utah.
Top




 Ha, C. S., Plesha, M. E., Lakes, R. S., Chiral three-dimensional isotropic lattices with negative Poisson's ratio, Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055
Ha, C. S., Plesha, M. E., Lakes, R. S., Chiral three-dimensional isotropic lattices with negative Poisson's ratio, Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055